Generalized Linear Models in R
May 2021
1 Overview of GLMs
This article will introduce you to specifying the the link and variance function for a generalized linear model (GLM, or GzLM). The article provides example models for binary, Poisson, quasi-Poisson, and negative binomial models. The article also provides a diagnostic method to examine the variance assumption of a GLM model.
1.1 Preliminaries
You will get the most from this article if you follow along with the examples in RStudio. Working the exercise will further enhance your skills with the material.
To prepare your RStudio session, paste the code below into a script, which you can save as “glm.R”. Then, run the code.
library(faraway) # for the hsb dataset
library(MASS) # for negative binomial support
library(ggplot2) # for plotting1.2 GLM families
GLMs are useful when the range of your response variable is constrained and/or the variance is not constant or normally distributed. GLM models transform the response variable to allow the fit to be done by least squares. The transformation done on the response variable is defined by the link function. This transformation of the response may constrain the range of the response variable. The variance function specifies the relationship of the variance to the mean. In R, a family specifies the variance and link functions which are used in the model fit. As an example the “poisson” family uses the “log” link function and “\(\mu\)” as the variance function. A GLM model is defined by both the formula and the family.
GLM models can also be used to fit data in which the variance is proportional to one of the defined variance functions. This is done with quasi families, where Pearson’s \(\chi^2\) (“chi-squared”) is used to scale the variance. An example would be data in which the variance is proportional to the mean. This would use the “quasipoisson” family. This results in a variance function of \(\alpha\mu\) instead of \(1\mu\) as for Poisson distributed data. The quasi families allows inference to be done when your data is overdispersed or underdispersed, provided that the variance is proportional.
The default link function for a family can be changed by specifying a link to the family function. For example, if the response variable is non negative and the variance is proportional to the mean, you would use the “identity” link with the “quasipoisson” family function. This would be specified as
family = quasipoisson(link = "identity")The decision of which family is appropriate is not discussed in this series.
1.3 GLM model evaluation
GLM models have a defined relationship between the expected variance and the mean. This relationship can be used to evaluate the model’s goodness of fit to the data. The deviance can be used for this goodness of fit check. Under asymptotic conditions the deviance is expected to be \(\chi^2_{df}\) distributed. Pearson’s \(\chi^2\) can also be used for this measure of goodness of fit, though technically it is the deviance which is minimized when fitting a GLM model.
There are some limits to the goodness of fit evaluation.
- When the response data is binary, the deviance approximations are not even approximately correct.
- The deviance approximations are also not useful when there are small group sizes.
- The goodness of fit tests using deviance or Pearson’s \(\chi^2\) are not applicable with a quasi family model.
Residual plots are useful for some GLM models and much less useful for others. When residuals are useful in the evaluation a GLM model, the plot of Pearson residuals versus the fitted link values is typically the most helpful. The Pearson residuals are normalized by the variance and are expected to then be constant across the prediction range. Pearson residuals and the fitted link values are obtained by the extractor functions residuals() and predict(), each of which has a type argument that determines what values are returned:
residuals(modObj, type = "resType")returns a vector of the residuals. “resType” can be set to “deviance”, “pearson”, “working”, “response”, or “partial”.predict(modObj, type = "fitType")returns a vector of fitted values. “fitType” can be set to “link”, “response”, or “terms”.
1.4 Variable selection
Variable selection for a GLM model is similar to the process for an OLS model. Nested model tests for significance of a coefficient are preferred to Wald test of coefficients. This is due to GLM coefficients standard errors being sensitive to even small deviations from the model assumptions. It is also more accurate to obtain p-values for the GLM coefficients from nested model tests.
The likelihood ratio test (LRT) is typically used to test nested models. For quasi family models an F-test is used for nested model tests (or when the fit is overdispersed or underdispersed). This use of the F statistic is appropriate if the group sizes are approximately equal.
Which variable to select for a model may depend on the family that is being used in the model. In these cases variable selection is connected with family selection. Variable selection criteria such as AIC and BIC are generally not applicable for selecting between families.
1.5 Binary response variable (Logistic)
Binary data, like binomial data, is typically modeled with the logit link and variance function \(\mu(1-\mu)\). The modeled response is the predicted log odds of an event.
We will use the hsb dataset from the faraway package for our binary response model. This dataset is a subset of a National Education Longitudinal Studies dataset. We will start by loading the dataframe and taking a look at the variables.
Enter the following commands in your script and run them.
data(hsb)
str(hsb)## 'data.frame': 200 obs. of 11 variables:
## $ id : int 70 121 86 141 172 113 50 11 84 48 ...
## $ gender : Factor w/ 2 levels "female","male": 2 1 2 2 2 2 2 2 2 2 ...
## $ race : Factor w/ 4 levels "african-amer",..: 4 4 4 4 4 4 1 3 4 1 ...
## $ ses : Factor w/ 3 levels "high","low","middle": 2 3 1 1 3 3 3 3 3 3 ...
## $ schtyp : Factor w/ 2 levels "private","public": 2 2 2 2 2 2 2 2 2 2 ...
## $ prog : Factor w/ 3 levels "academic","general",..: 2 3 2 3 1 1 2 1 2 1 ...
## $ read : int 57 68 44 63 47 44 50 34 63 57 ...
## $ write : int 52 59 33 44 52 52 59 46 57 55 ...
## $ math : int 41 53 54 47 57 51 42 45 54 52 ...
## $ science: int 47 63 58 53 53 63 53 39 58 50 ...
## $ socst : int 57 61 31 56 61 61 61 36 51 51 ...We will model the odds of a student’s program of choice being “academic” as our response variable. We will use all the other variables in the dataset as independent variables. We will ignore interactions here to focus on the GLM fitting process.
Enter the following commands in your script and run them.
g1 <- glm(I(prog == "academic") ~ gender + race + ses + schtyp + read + write + science + socst,
family = binomial(),
data = hsb)
summary(g1)##
## Call:
## glm(formula = I(prog == "academic") ~ gender + race + ses + schtyp +
## read + write + science + socst, family = binomial(), data = hsb)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.1823 -0.8645 0.3223 0.8676 2.0749
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -4.94995 1.49602 -3.309 0.000937 ***
## gendermale 0.23634 0.37889 0.624 0.532779
## raceasian -0.11219 0.92526 -0.121 0.903490
## racehispanic 0.52553 0.71902 0.731 0.464842
## racewhite -0.14508 0.61364 -0.236 0.813101
## seslow -0.69719 0.51813 -1.346 0.178437
## sesmiddle -0.90940 0.41622 -2.185 0.028896 *
## schtyppublic -1.16715 0.49695 -2.349 0.018843 *
## read 0.06760 0.02596 2.604 0.009208 **
## write 0.05920 0.02801 2.114 0.034540 *
## science -0.05286 0.02612 -2.023 0.043029 *
## socst 0.05148 0.02259 2.279 0.022648 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 276.76 on 199 degrees of freedom
## Residual deviance: 211.26 on 188 degrees of freedom
## AIC: 235.26
##
## Number of Fisher Scoring iterations: 4The summary output for a GLM models displays the call, residuals, and coefficients, similar to the summary of an object fit with lm(). However, the model information at the bottom of the output is different. For a GLM model, the dispersion parameter and deviance values are provided. Here we have a set dispersion value of 1, since we are not working with a quasi family.
We will not check the model fit with a test of the residual deviance, since the distribution is not expected to be \(\chi^2_{df}\) distributed.
Instead, we will use step() with the criteria being the LRT to reduce unneeded variables from the model.
Enter the following command in your script and run it.
step(g1, test="LRT")## Start: AIC=235.26
## I(prog == "academic") ~ gender + race + ses + schtyp + read +
## write + science + socst
##
## Df Deviance AIC LRT Pr(>Chi)
## - race 3 212.64 230.64 1.3789 0.710487
## - gender 1 211.65 233.65 0.3906 0.531964
## <none> 211.26 235.26
## - ses 2 216.23 236.23 4.9660 0.083492 .
## - science 1 215.52 237.52 4.2646 0.038916 *
## - write 1 215.90 237.90 4.6386 0.031260 *
## - socst 1 216.66 238.66 5.4048 0.020082 *
## - schtyp 1 217.29 239.29 6.0261 0.014096 *
## - read 1 218.41 240.41 7.1487 0.007502 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Step: AIC=230.64
## I(prog == "academic") ~ gender + ses + schtyp + read + write +
## science + socst
##
## Df Deviance AIC LRT Pr(>Chi)
## - gender 1 213.18 229.18 0.5399 0.46246
## <none> 212.64 230.64
## - ses 2 217.43 231.43 4.7867 0.09132 .
## - write 1 217.06 233.06 4.4201 0.03552 *
## - schtyp 1 218.19 234.19 5.5518 0.01846 *
## - science 1 218.20 234.20 5.5653 0.01832 *
## - socst 1 218.33 234.33 5.6894 0.01707 *
## - read 1 219.39 235.39 6.7547 0.00935 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Step: AIC=229.18
## I(prog == "academic") ~ ses + schtyp + read + write + science +
## socst
##
## Df Deviance AIC LRT Pr(>Chi)
## <none> 213.18 229.18
## - ses 2 218.13 230.13 4.9494 0.084189 .
## - write 1 217.06 231.06 3.8857 0.048700 *
## - science 1 218.25 232.25 5.0752 0.024271 *
## - schtyp 1 218.78 232.78 5.6008 0.017953 *
## - socst 1 218.85 232.85 5.6742 0.017216 *
## - read 1 220.55 234.55 7.3690 0.006636 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call: glm(formula = I(prog == "academic") ~ ses + schtyp + read + write +
## science + socst, family = binomial(), data = hsb)
##
## Coefficients:
## (Intercept) seslow sesmiddle schtyppublic read
## -4.38958 -0.67766 -0.89902 -1.10394 0.06794
## write science socst
## 0.04845 -0.05345 0.05174
##
## Degrees of Freedom: 199 Total (i.e. Null); 192 Residual
## Null Deviance: 276.8
## Residual Deviance: 213.2 AIC: 229.2We can now fit the model suggested by step(), found near the bottom of the output.
Enter the following commands in your script and run them.
g2 <- glm(I(prog == "academic") ~ ses + schtyp + read + write + science + socst,
family = "binomial",
data = hsb)
summary(g2)##
## Call:
## glm(formula = I(prog == "academic") ~ ses + schtyp + read + write +
## science + socst, family = "binomial", data = hsb)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.1132 -0.8912 0.3224 0.8909 2.0947
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -4.38958 1.37564 -3.191 0.00142 **
## seslow -0.67766 0.49931 -1.357 0.17472
## sesmiddle -0.89902 0.41186 -2.183 0.02905 *
## schtyppublic -1.10394 0.48643 -2.269 0.02324 *
## read 0.06794 0.02570 2.644 0.00820 **
## write 0.04845 0.02494 1.942 0.05210 .
## science -0.05345 0.02434 -2.196 0.02810 *
## socst 0.05174 0.02214 2.337 0.01946 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 276.76 on 199 degrees of freedom
## Residual deviance: 213.18 on 192 degrees of freedom
## AIC: 229.18
##
## Number of Fisher Scoring iterations: 4Note there are differences between the p-values reported in summary and what was reported the the LRT test in the final step of the step() function above.
The quasi-binomial family is useful for modeling response variables with a bounded range.
1.5.1 Diagnostics
Residual plots provide little assistance in evaluating binary models. The diagnostics for the sensitivity of the model to the data are checked checked using the same methods as is done for OLS models. See the article on Regression Diagnostics.
1.6 Count response variable
Count data is typically modeled using the Poisson family. This uses a log link function and a variance function of \(\mu\). The modeled response is the predicted log count.
We will use the discoveries dataset from the datasets package for our binary response model. This dataset is the number of great inventions for the years 1860 to 1959. We will start by loading the dataframe and adding a variable to represent the number of years since 1860. We will assume that there is no correlation between the years to focus on the GLM model fit.
Enter the following commands in your script and run them.
data(discoveries)
disc <- data.frame(count = as.numeric(discoveries),
year = seq(0, (length(discoveries) - 1)))We will fit the count of inventions with year and year squared.
Enter the following commands in your script and run them.
yearSqr <- disc$year^2
p1 <- glm(count ~ year + yearSqr,
family = "poisson",
data = disc)
summary(p1)##
## Call:
## glm(formula = count ~ year + yearSqr, family = "poisson", data = disc)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.9066 -0.8397 -0.2544 0.4776 3.3303
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 7.592e-01 1.814e-01 4.186 2.84e-05 ***
## year 3.356e-02 8.499e-03 3.948 7.87e-05 ***
## yearSqr -4.106e-04 8.699e-05 -4.720 2.35e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 164.68 on 99 degrees of freedom
## Residual deviance: 132.84 on 97 degrees of freedom
## AIC: 407.85
##
## Number of Fisher Scoring iterations: 5We can check the goodness of fit of this model. We will use the deviance of the residuals for this test.
Enter the following commands in your script and run them.
1 - pchisq(deviance(p1), df.residual(p1))## [1] 0.009204575The p-value is approximately .001. This deviance is not likely to have occurred by chance, under the null hypothesis of the deviances being \(\chi^2\). Therefore we have evidence of overdispersion. The presence of overdispersion suggested the use of the F-test for nested models. We will test if the squared term can be dropped from the model.
Enter the following command in your script and run it.
drop1(p1, test = "F")## Warning in drop1.glm(p1, test = "F"): F test assumes 'quasipoisson' family## Single term deletions
##
## Model:
## count ~ year + yearSqr
## Df Deviance AIC F value Pr(>F)
## <none> 132.84 407.85
## year 1 149.66 422.67 12.286 0.0006927 ***
## yearSqr 1 157.32 430.32 17.874 5.345e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The p-value for yearSqr is small (.0005), so we will retain the yearSqr term in the model.
1.6.1 Quasi-Poisson model
The invention count model from above needs to be fit using the quasi-Poisson family, which will account for the greater variance in the data.
Enter the following commands in your script and run them.
p2 <- glm(count ~ year + yearSqr,
family = "quasipoisson",
data = disc)
summary(p2)##
## Call:
## glm(formula = count ~ year + yearSqr, family = "quasipoisson",
## data = disc)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.9066 -0.8397 -0.2544 0.4776 3.3303
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.7592473 0.2072715 3.663 0.000406 ***
## year 0.0335569 0.0097112 3.455 0.000816 ***
## yearSqr -0.0004106 0.0000994 -4.131 7.66e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 1.305649)
##
## Null deviance: 164.68 on 99 degrees of freedom
## Residual deviance: 132.84 on 97 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 5There is no change in the estimated coefficients between the quasi-Poisson fit and the Poisson fit. The significance of the terms does change, but a dispersion parameter is estimated.
Before determining that the quasi-Poisson family is appropriate, we will check to see if the variance of the residuals is proportional to the mean. We begin this check by creating a new dataframe which includes the residuals and fitted values.
Enter the following command in your script and run it.
p1Diag <- data.frame(disc,
link = predict(p1, type = "link"),
fit = predict(p1, type = "response"),
pearson = residuals(p1, type = "pearson"),
resid = residuals(p1, type = "response"),
residSqr = residuals(p1, type = "response")^2
)We will plot the square of the residual against the predicted mean. We will add to this scatter plot a black line for the Poisson-assumed variance (the mean), a dashed green line for the quasi-Poisson assumed variance, and a blue curve for the smoothed mean of the square of the residual.
Enter the following command in your script and run it.
ggplot(p1Diag, aes(x = fit, y = residSqr)) +
geom_point() +
geom_abline(intercept = 0, slope = 1, size = 1) +
geom_abline(intercept = 0, slope = summary(p2)$dispersion,
color = "darkgreen", linetype = 2, size = 1) +
geom_smooth(se = F, size = 1) +
theme_bw() ## `geom_smooth()` using method = 'loess' and formula 'y ~ x'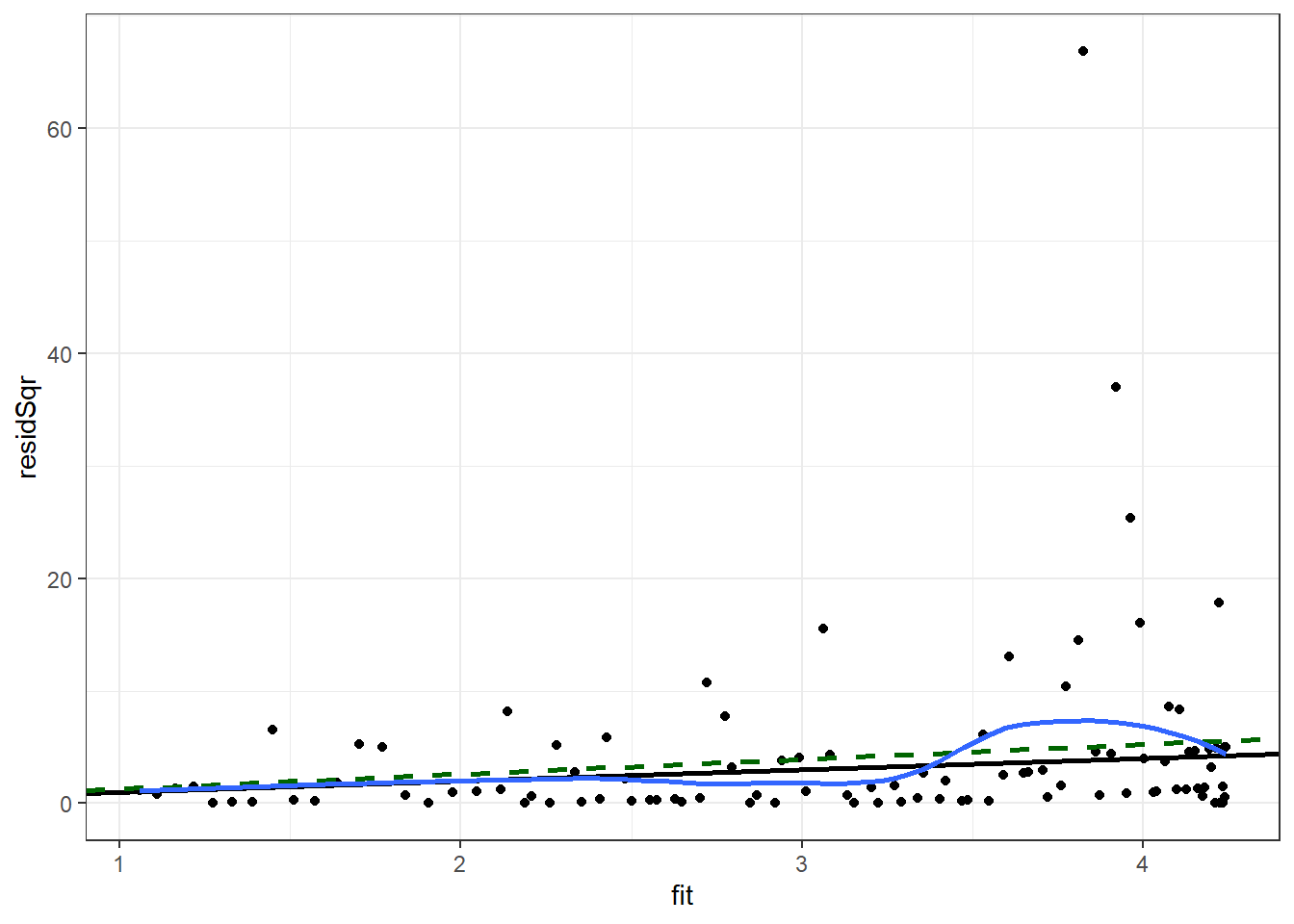
Ideally the blue curve would be straight and it would be collinear with the green line for the quasi-Poisson variance. The greater the deviation from the green line the greater the concern is about the proportionality of the variance to the mean. Here we have some indication that the variance may not be proportional to the mean.
1.6.2 Negative binomial model
We will now look to see if a negative binomial model might be a better fit. The negative binomial requires the use of the glm.nb() function in the MASS package. The call to glm.nb() is similar to that of glm(), except no family is given.
Enter the following commands in your script and run them.
nb1 <- glm.nb(count ~ year + yearSqr,
data = disc)
summary(nb1)##
## Call:
## glm.nb(formula = count ~ year + yearSqr, data = disc, init.theta = 11.53157519,
## link = log)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.6849 -0.7707 -0.2344 0.4232 2.7134
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 7.526e-01 2.019e-01 3.727 0.000194 ***
## year 3.386e-02 9.471e-03 3.575 0.000350 ***
## yearSqr -4.132e-04 9.627e-05 -4.292 1.77e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for Negative Binomial(11.5316) family taken to be 1)
##
## Null deviance: 131.91 on 99 degrees of freedom
## Residual deviance: 106.20 on 97 degrees of freedom
## AIC: 406.21
##
## Number of Fisher Scoring iterations: 1
##
##
## Theta: 11.53
## Std. Err.: 7.42
##
## 2 x log-likelihood: -398.214The coefficients have only a small change from those of the quasi-Poisson model.
The drop1() function is used to test the significance of the squared term for year. We use the LRT for negative binomial models.
Enter the following command in your script and run it.
drop1(nb1, test = "LRT")## Single term deletions
##
## Model:
## count ~ year + yearSqr
## Df Deviance AIC LRT Pr(>Chi)
## <none> 106.20 404.21
## year 1 119.54 415.55 13.338 0.00026 ***
## yearSqr 1 125.79 421.80 19.589 9.602e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The squared term is significant and is retained in the model.
We will repeat the check of the variance of the residuals which was done for the quasi-Poisson model. Plotting the square of the residual to the fitted values, with a black line for Poisson, a dashed green line for quasi-Poisson, a blue curve for smoothed mean of the square of the residual, and a red curve for predicted variance from the negative binomial fit.
Enter the following command in your script and run it.
nb1Diag <- data.frame(disc,
link = predict(nb1, type = "link"),
fit = predict(nb1, type = "response"),
pearson = residuals(nb1,type = "pearson"),
resid = residuals(nb1,type = "response"),
residSqr = residuals(nb1,type = "response")^2
)
ggplot(nb1Diag, aes(x = fit, y = residSqr)) +
geom_point() +
geom_abline(intercept = 0, slope = 1, size = 1) +
geom_abline(intercept = 0, slope = summary(p2)$dispersion,
color = "darkgreen", linetype = 2, size = 1) +
stat_function(fun = function(fit) {fit + fit^2 / 11.53},
color = "red", size = 1) +
geom_smooth(se = F, size = 1) +
theme_bw() ## `geom_smooth()` using method = 'loess' and formula 'y ~ x'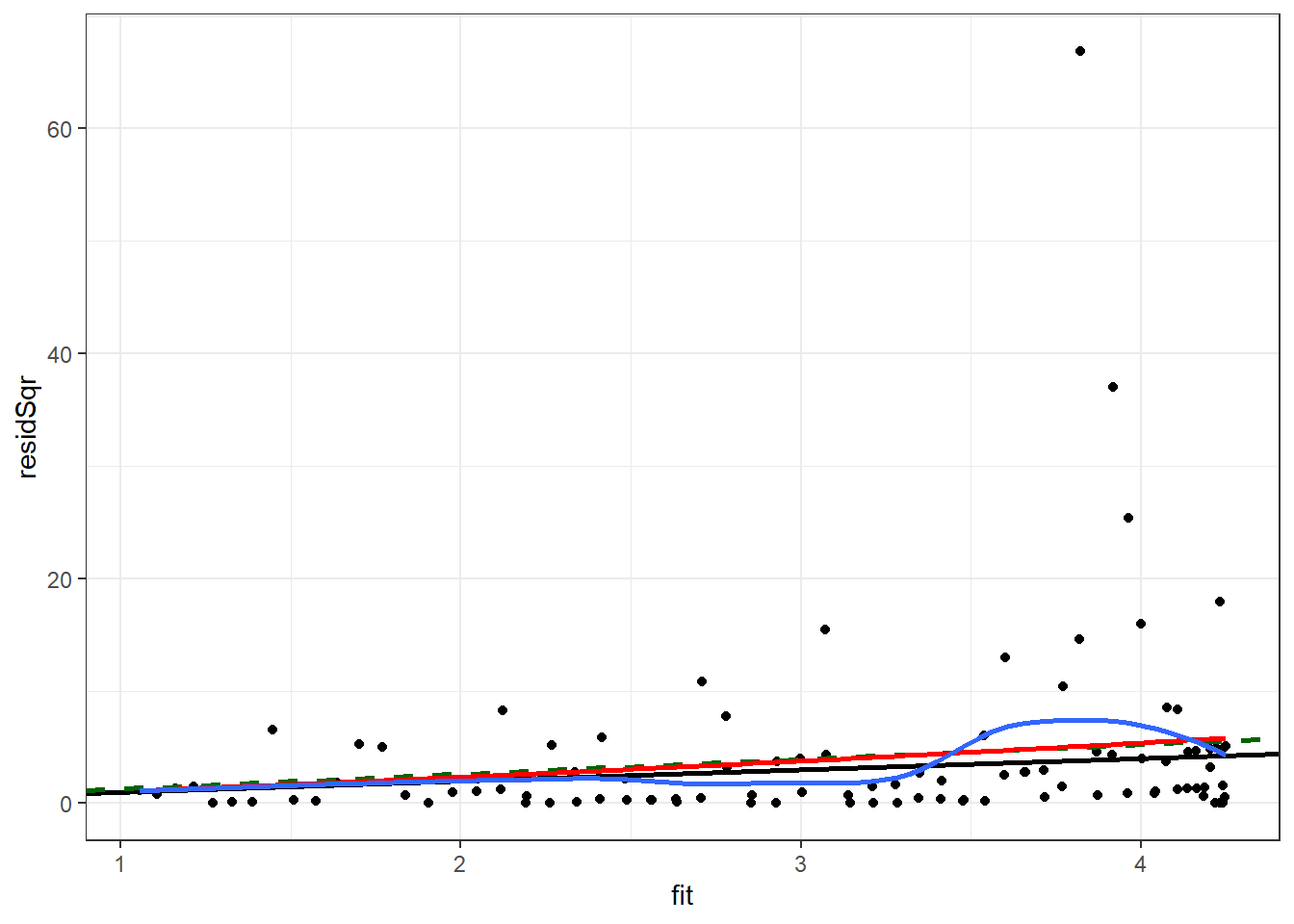
The negative binomial variance curve (red) is close to the quasi-Poisson line (green).
Although the means and variance predictions for the negative binomial and quasi-Poisson models are similar, the probability for any given integer is different for the two models. The following code shows the predicted probabilities of 0 through 7 when the mean is predicted to be 4.
Enter the following command in your script and run it.
data.frame(number=0:8,
prob_Poisson = round(dpois(0:8,
(4*summary(p2)$dispersion)),
3),
prob_NBinom = round(dnbinom(0:8,
mu=4,
size=summary(nb1)$theta),
3)
)## number prob_Poisson prob_NBinom
## 1 0 0.005 0.032
## 2 1 0.028 0.096
## 3 2 0.074 0.155
## 4 3 0.128 0.180
## 5 4 0.167 0.168
## 6 5 0.175 0.134
## 7 6 0.152 0.095
## 8 7 0.113 0.062
## 9 8 0.074 0.037summary(nb1)$theta## [1] 11.53158The interpretation of the two models is different as well as the probabilities of the event counts. Examining the diagnostics would be useful step in choosing between these two models.
1.6.3 Diagnostics
Residual plots of the Pearson residuals to the link function have some utility for count data. The diagnostics for the sensitivity of the model to the data are checked using the same methods as is done for OLS models.
1.7 Exercises
Use the following code to load the
warpbreaksdata set and examine the variables in the data set.data(warpbreaks) str(warpbreaks) plot(warpbreaks)Use the Poisson family and fit breaks with
wool,tension, and their interaction.Check to see if this is an appropriate model. If not, choose a more appropriate model form.
Use the backward selection method to reduce your model, if possible. Use your model from the prior problem as the starting model.
Check the residual variance assumption for your model.