This article will teach you the fundamentals of running regressions in Stata. We'll use the auto data set that comes with Stata throughout. Start a do file as usual, and save it as regression.do:
clear all
capture log close
set more off
log using regression.log, replace
sysuse auto
//real work goes here
log close
Remember the code you add goes after sysuse auto and before log close.
Stata has many, many commands for doing various kinds of regressions, but its developers worked hard to make them all as similar as possible. Thus if you can do a simple linear regression you can do all sorts of more complex models.
Linear Regression
The regress (reg) command does linear regression. It always needs a varlist, and it uses it in a particular way: the first variable is the dependent variable, and it is regressed on all the others in the list plus a constant (unless you add the noconstant option).
Let's estimate how much consumers were willing to pay for good gas mileage in 1978 using a naive "hedonic pricing" model (i.e., we'll presume the price depends on the characteristics of the car). Whether a car is foreign or domestic seems to be important, so throw that in as a covariate too. Type:
regress price mpg foreign
This regresses price on mpg and foreign. The negative and highly significant coefficient on mpg suggests that American consumers in 1978 disliked fuel efficiency, and would pay to avoid it!
Like any good researcher, when our empirical results contradict our theory (or common sense) we first look for better empirical results. We might possibly have some missing variable bias here; in particular it's probably important to control for the size of the car by adding weight to the regression:
reg price mpg foreign weight
Now mpg is insignificant but weight is positive and highly significant. Looks like American consumers in 1978 liked big cars and didn't care about fuel efficiency, a much more plausible result.
Logistical Regression
Logistical regression is just as easy to run, but we need a binary dependent variable. Make an indicator variable goodRep which is one for cars with rep78 greater than three (and missing if rep78 is missing):
gen goodRep = (rep78>3) if rep78<.
Now let's examine what predicts a car's repair record. We'll include displacement and gear_ratio because they're the only technical data we have about the car's engine (the most likely thing to break), weight as a measure of load on the engine, foreign just because it seems to be an important characteristic of a car. There are other variables that may seem like good candidates for predictors, but keep in mind you only have 74 observations. A good rule of thumb for logistic regression is that you need at least 15 observations per predictor and hopefully many more.
The logit command runs logistical regression. The syntax is identical to regress:
logit goodRep displacement gear_ratio weight foreign
If you prefer odds ratios to coefficient add the or option. Just be sure to interpret them properly, as well discuss later. The fact that logit models are easy to run often masks the fact that they can be extremely difficult to interpret.
Categorical (Factor) Variables
Consider the variable rep78: it is a measure of the car's repair record and takes on the values one through five (plus a few missing values). However, these numbers only represent categories—a car with a rep78 of five is not five times better than a car with a rep78 of one. Thus it would make no sense to include rep78 in a regression as-is. However, you might want to include a set of indicator variables, one for each value of rep78. This is even more important for categorical variables with no underlying order, like race. Stata can create such indicator variables for you "on the fly"; in fact you can treat them as if they were always there.
The set of indicator variables representing a categorical variable is formed by putting i. in front of the variable's name. This works in most (but not all) varlists. To see how it works, try:
list rep78 i.rep78
As you see, 3.rep78 is one if rep78 is three and zero otherwise. The other indicators are constructed in the same way. 1b.rep78 is a special case: it is the base category, and always set to zero to avoid the "dummy variable trap" in regressions. If rep78 is missing, all the indicator variables are also missing.
If you want to choose a different category as the base, add b and then the number of the desired base category to the i:
list rep78 ib3.rep78
Now try using i.rep78 in a regression:
reg price weight foreign i.rep78
The coefficients for each value of rep78 are interpreted as the expected change in price if a car moved to that value of rep78 from the base value of one. If you change the base category:
reg price weight ib3.rep78
the model is the same, but the coefficients are now the expected change in price if a car moves to that value of rep78 from a rep78 of three. You can verify that the models are equivalent by noting that the coefficients in the second model are just the coefficients of the first model minus the coefficient for 3.rep78 from the first model.
You don't have to use the full set of indicators. For example, you could pick out just the indicator for rep78 is five with:
reg price weight 5.rep78
This has the effect of collapsing all the other categories into a single category of "not five."
Indicator variables are, in a sense, categorical variables. Marking them as such will not affect your regression output; you'll get the same results from:
reg price weight ib3.rep78 foreign
as from:
reg price weight ib3.rep78 i.foreign
However, the latter tells Stata that foreign is not continuous, which is very important to some postestimation commands. However, if you're not planning to run margins or some other postestimation command that cares about this distinction, putting foreign in your model rather than i.foreign is just fine.
Interactions
You can add interactions between variables by putting two pound signs between them:
reg price weight foreign##rep78
The two pound signs means "include the main effects of foreign and rep78 and their interactions." Two variables with one pound sign between them refers to just their interactions. It's almost always a mistake to include interactions in a regression without the main effects, but you'll need to talk about the interactions alone in some postestimation commands.
The variables in an interaction are assumed to be categorical unless you say otherwise. Thus the above model includes everything in:
reg price weight i.foreign i.rep78
What it adds is a new set of indicator variables, one for each unique combination of foreign and rep78. This allows the model to see, for example, whether the effect of having a rep78 of five is different for foreign cars than for domestic cars.
Note that while Stata chose rep78==1 for its base category, it had to drop the rep78==5 category for foreign cars because no foreign cars have a rep78 of one. If you'd prefer that it drop the same category for both types of cars, choose a different base category:
reg price weight foreign##ib3.rep78
To form interactions involving a continuous variable, use the same syntax but put c. in front of the continuous variable's name:
reg price foreign##c.weight i.rep78
This allows the effect of weight on price to be different for foreign cars than for domestic cars (i.e. they can have different slopes).
The ## symbol is an operator just like + or -, so you can use parentheses with the usual rules:
reg price foreign##(c.weight rep78)
This interacts foreign with both weight and rep78. The latter is automatically treated as a categorical variable since it appears in an interaction and does not have c. in front of it.
Interactions are formed by multiplication: to form an indicator for "car is foreign and has a rep78 of 5" multiply an indicator for "car is foreign" by an indicator for "car has a rep78 of 5." But this is not limited to indicators:
reg price c.weight##c.weight
This regresses price on weight and weight squared, allowing you to consider non-linear effects of weight (at least second order Taylor series approximations to them). You could estimate the same model with:
gen weightSquared=weight^2
reg price weight weightSquared
Specifying the model using interactions is shorter, obviously. But it also (again) helps postestimation commands understand the structure of the model.
Exercises
- The product of weight and mpg measures how many pounds a car's engine can move one mile using one gallon of gasoline, and is thus a measure of the efficiency of the engine independent of the car it's placed in. Regress the price of a car on this product and the main effects of weight and mpg. Form the product of weight and mpg using interactions, not gen. Hint: if you get an error message, read it carefully. (Solution)
- Suppose I argued that "The efficiency of an engine in terms of pound-miles per gallon is an attribute of the engine, not an interaction. Thus I don't need to include the main effects of weight and mpg." Run that model, then explain how the results of that model compared to one that includes main effects of weight and mpg (i.e. the model from exercise 1) show that this argument is wrong. (Solution)
Postestimation
Estimation commands store values in the e vector, which can be viewed with the ereturn list command. Try:
reg price c.weight##c.weight i.foreign i.rep78 mpg displacement
ereturn list
Most of these results are only of interest to advanced Stata users, with one important exception.
The e(sample) function tells you whether a particular observation was in the sample used for the previous regression. It is 1 (true) for observations that were included and 0 (false) for observations that were not. In this case, the five observations with missing values of rep78 were excluded. e(sample) can be very useful if you think missing data may be causing problems with your model. For example, you could type:
tab foreign if e(sample)
to check which values of foreign actually appear in the data used in the regression. Or:
sum mpg if e(sample)
sum mpg if !e(sample)
will tell you if the mean value of mpg is different for the observations used than for the observations not used, which could indicate that the data are not missing at random.
Regression coefficients are stored in the e(b) matrix. We won't discuss working with matrices, but they are also available as _b[var] (e.g. _b[mpg]). Standard errors are available as _se[var].
Most of the time you won't use the e vector directly. Instead you'll use Stata's postestimation commands and let them work with the e vector. We'll cover just a small sample of them.
Hypothesis Tests on Coefficients
The test command tests hypotheses about the model coefficients. The syntax is just test plus a list of hypotheses, which are tested jointly. In setting up hypotheses, the name of a variable is taken to mean the coefficient on that variable. If you just give the name of a variable without comparing it to something, test will assume you want to test the hypothesis that that variable's coefficient is zero. The command:
test mpg displacement
tests the hypothesis that the coefficients on mpg and displacement are jointly zero. If you want to jointly test more complicated hypotheses, put each hypothesis in parentheses:
test (mpg==-50) (displacement==5)
For factor variables, indicate which level you want to test by putting the number before the variable, followed by a period:
test 1.foreign=3000
For interactions, use the variable name itself to refer to the main effect, and the interaction specified with one pound sign for the interaction term:
test weight c.weight#c.weight
You can have variables on both sides of the equals sign:
test weight=mpg
This is equivalent to (and will be recast as):
test weight-mpg==0
Predicted Values
The predict command puts the model's predicted values in a variable:
predict phat
("hat" refers to the circumflex commonly used to denote estimated values). You can calculate residuals with the residuals option:
predict res, residuals
You can change your data between running the model and making the predictions, which means you can look at counterfactual scenarios like "What if all the cars were foreign?" See Making Predictions with Counter-Factual Data in Stata for some examples. However, it's usually easier to do that kind of thing using margins.
Margins
The margins command is a very useful tool for exploring what your regression results mean.
If you just type:
margins
all by itself, Stata will calculate the predicted value of the dependent variable for each observation, then report the mean value of those predictions (along with the standard error, t-statistic, etc.).
If margins is followed by a categorical variable, Stata first identifies all the levels of the categorical variable. Then, for each value it calculates what the mean predicted value of the dependent variable would be if all observations had that value for the categorical variable. All other variables are left unchanged. Thus:
margins foreign
first asks, "What would the mean price be if all the cars were domestic?" (but still had their existing weights, displacements, etc.) and then asks "What would the mean price be if all the cars were foreign?"
margins rep78
does the same for all five values of rep78, but since there are so many of them it's a good candidate for a graphical presentation. The marginsplot command takes the results of the previous margins command and turns them into a graph:
marginsplot
For continuous variables margins obviously can't look at all possible values, but you can specify which values you want to examine with the at option:
margins, at(weight=(2000 4000))
This calculates the mean predicted value of price with weight set to 2000 pounds, and then again with weight set to 4000 pounds. Think of each value as a "scenario"—the above scenarios are very simple, but you can make much more complicated scenarios by listing multiple variables and values in the at option. The margins output first assigns a number to each scenario, then gives their results by number.
The values are specified using a numlist. A numlist is a list of numbers just like a varlist is a list of variables and, like a varlist, there are many different ways to define a numlist. Type help numlist to see them all. The simplest method is just to list the numbers you want, as above. We'll learn one more version, which is start (interval) end:
margins, at(weight=(1500 (500) 5000))
This calculates the mean predicted value of price with weight set to 1500, 2000, 2500, etc. up to 5000. (The actual weights range from 1760 to 4840.) Again, this is a good candidate for a graphic:
marginsplot
If you want to look at the marginal effect of a covariate, or the derivative of the mean predicted value with respect to that covariate, use the dydx option:
margins, dydx(mpg)
In this simple case, the derivative is just the coefficient on mpg, which will always be the case for a linear model. But consider changing weight: since the model includes both weight and weight squared you have to take into account the fact that both change. This case is particularly confusing (but not unusual) because the coefficient on weight is negative but the coefficient on weight squared is positive. Thus the net effect of changing weight for any given car will very much depend on its starting weight.
The margins command can very easily tell you the mean effect:
margins, dydx(weight)
What margins does here is take the numerical derivative of the expected price with respect to weight for each car, and then calculates the mean. In doing so, margins looks at the actual data. Thus it considers the effect of changing the Honda Civic's weight from 1,760 pounds as well as changing the Lincoln Continental's from 4,840 (the weight squared term is more important with the latter than the former). It then averages them along with all the other cars to get its result of 2.362865, or that each additional pound of weight increases the mean expected price by $2.36.
To see how the effect of weight changes as weight changes, use the at option again and then plot the results:
margins, dydx(weight) at(weight=(1500 (500) 5000))
marginsplot
This tells us that for low values of weight (less than about 2000), increasing weight actually reduces the price of the car. However, for most cars increasing weight increases price.
The dydx option also works for binary variables:
margins, dydx(foreign)
However, because foreign was entered into the model as i.foreign, margins knows that it cannot take the derivative with respect to foreign (i.e. calculate what would happen if all the cars became slightly more foreign). Thus it reports the difference between the scenario where all the cars are foreign and the scenario where all the cars are domestic. You can verify this by running:
margins foreign
and doing the subtraction yourself.
Binary Outcome Models and Predicted Probabilities
The margins command becomes even more useful with binary outcome models because they are always nonlinear. Clear the auto data set from memory and then load grad:
clear
use http://ssc.wisc.edu/sscc/stata/grad.dta
This is a fictional data set consisting of 10,000 students. Exactly one half of them are "high socioeconomic status" (highSES) and one half are not. Exactly one half of each group was given an intervention, or "treatment" (treat) designed to increase the probability of graduation. The grad variable tells us whether they did in fact graduate. Your goals are to determine 1) whether the treatment made any difference, and 2) whether the effect of the treatment differed by socioeconomic status (SES).
You can answer the first question with a simple logit model:
logit grad treat highSES
The coefficient on treat is positive and significant, suggesting the intervention did increase the probability of graduation. Note that highSES had an even bigger impact.
Next examine whether the effect depends on SES by adding an interaction between the two:
logit grad treat##highSES
The coefficient on treat#highSES is not significantly different from zero. But does that really mean the treatment had exactly the same effect regardless of SES?
Binary outcomes are often interpreted in terms of odds ratios, so repeat the previous regression with the or option to see them:
logit grad treat##highSES, or
This tells us that the odds of graduating if you are treated are approximately 2.83 times the odds of graduating if you are not treated, regardless of your SES. Researchers sometimes confuse odds ratios with probability ratios; i.e. they say you are 2.83 times more "likely" to graduate if you are treated. This is incorrect.
If you ask margins to examine the interaction between two categorical variables, it will create scenarios for all possible combinations of those variables. You can use this to easily obtain the predicted probability of graduation for all four possible scenarios (high SES/low SES, treated/not treated):
margins highSES#treat
For low SES students, treatment increases the predicted probability of graduation from about .49 to about .73. For high SES students, treatment increases the predicted probability of graduation from about .96 to about .98. Now, if you plug those probabilities into the formula for calculating the odds ratio, you will find that the odds ratio is 2.83 in both cases (use the full numbers from the margins output, not the two digit approximations given here). Treatment adds the same amount to the linear function that is passed through the logistic function in both cases. But recall the shape of the logistic function:
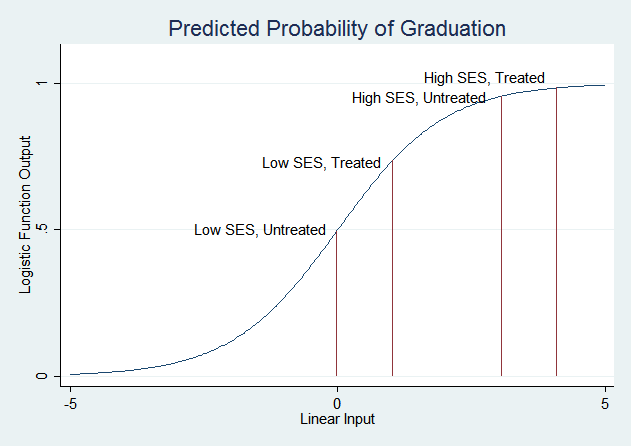
The treatment has a much smaller effect on the probability of graduation for high SES students because their probability is already very high—it can't get much higher. Low SES students are in the part of the logistic curve that slopes steeply, so changes in the linear function have much larger effects on the predicted probability.
The margins command can most directly answer the question "Does the effect of the treatment vary with SES?" with a combination of dydx() and at():
margins, dydx(treat) at(highSES=(0 1))
(You can also do this with margins highSES, dydx(treat).) Once again, these are the same numbers you'd get by subtracting the levels obtained above. We suggest always looking at levels as well as changes—knowing where the changes start from gives you a much better sense of what's going on.
What if you just ran:
margins, dydx(treat)
This examines the change in predicted probability due to changing the treat variable, but highSES is not specified so margins uses the actual values of highSES in the data and takes the mean across observations. Since our sample is about one half high SES and one half low, the mean change is 1/2 times the change for highSES students plus 1/2 times the change for low SES students. But if a sample had a different proportion of high and low SES students, this number would be very different. Any time the margins command does not specify values for all the variables in the underlying regression model, the result will only be valid for populations that are similar to the sample.
It's a general rule that it's easiest to change the predicted probability for subjects who are "on the margin;" i.e. those whose predicted probability starts near 0.5. However, this is a property of the logistic function, not the data. It is an assumption you make when you choose to run a logit model.
Exercises
- Try regressing price on weight, foreign and rep78, ignoring the fact that rep78 is a categorical variable. Then regress price on weight, foreign and i.rep78. Use the second model to test the hypothesis that the first model is right. (Hint: if it is right, what should the coefficients on the i.rep78 indicator variables in the second model be?) (Solution)
- Consider the final example of students and the treatment intended to increase the probability of graduation. Assume that these are the results from the first year of the program, and you are now deciding what to do in the second year. You can only give the treatment to one half of all the students, but you can choose which ones. If you are the superintendent of schools and will be evaluated based on your students' graduation rate, who do you want to give the treatment to? If you are the person administering the treatment program and will be evaluated based on the graduation rate of the students you treat, who do you want to give the treatment to? If you are the parent of a child in the district, who do you want to give the treatment to?
Last Revised: 5/4/2021